Batch 2 - Class 93 - Billiard Reflections
Pre-Class Problem:
- (Moscow - 235) A dying Roman, knowing his wife was pregnant, left a will saying that if she had a son, the son must get 2/3 of the inheritance and the widow must get 1/3. However, if she had a daughter, the widow must get 2/3 and daughter must get 1/3. Soon after his death, the widow had twins - a son and a daughter. How should the inheritance be divided as close as possible to the terms of the will?Answer: There is no single "right" answer:The father's intent is for a son to get twice as the mother, and the mother to get twice as much as the daughter. So you could divide the estate into 7 parts, give 4 to the son, 2 to mother and 1 to daughter.May be the father wished the mother to get at least 1/3, so could give her that. Then the son gets 4 times the daughter on the remaining estate, i.e. 4/5*2/3=8/15One of the twins must have been born first. If its the boy, give him 2/3 and then divide the remaining between widow and daughter in 2:1 ratio. Similarly, if the girl was born first.
Attendance: Anisha, Smiti, Muskaan, Tishyaa, Diya, Abhiram, Nandini, Liza, Khushi, Arnav, Anishka, Tara, Navya
Class Notes:
A ball is shot from the bottom left corner of, say, a 3x5 billiard table, for instance, at a 45 degree angle. The ball traverses the diagonals of individual squares drawn on the table, bouncing off the sides of the table at equal angles. Into which pocket, A, B, or C, will the ball eventually fall?
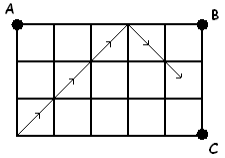
Experiment with tables of different dimensions. What do you notice about those tables that have the ball fall into pockets A, B, C? Test your theories with more tables.
- Instructor Notes: Some kids may start to get to the following conclusions (If not, let them try more and tabulate)If n and m are odd, the ball falls in pocket BIf n is even and m odd, the ball falls in pocket AIf n is odd and m even, the ball falls in pocket CIf both n and m are even, the equation is more complex. What is it?Must every ball land in either pocket A, B or C? Can the ball return to the start? Can the ball enter an infinite loop and never fall into a pocket?Instructor Note: Let kids play with the problem. After some time emphasize on the infinite loop problem. See if kids can get to the conclusion that balls never seem to come back to same path. Why? If balls get into a loop, consider the first cell where they started repeating the path - how do they get there? Can there be a "first" such cell?Could the ball enter the same square twice in opposite directions? Which is the first such cell?Could the ball pass the same square but along a different diagonal?If a ball can't traverse the same path (or reverse), what must eventually happen? What are the maximum possible diagonals the ball can pass through?Can it fall back into the lower left corner?
- Color the cells of each table black and red like a checkerboard. What do you notice about the path of a ball across red cells? Across black cells? Imagine a 13x29 table - do not draw. Imagine how a ball will traverse and where it can fall.The ball traverses red cells only along the northwest diagonals and black along southwest (or vice versa). How does that help you determine the square the ball can fall into?What if we color alternate vertices black and white? What can you deduce about the cells now?
.png)
- Can you start to explain the odd/even pattern now? What happens when n and m are both even?
- Can you take a 4x6 table and analyze the movement of the ball. Can you find an alternate (simpler) board where the movement looks exactly the same?
- With this "reduction", can you devise a rule for even by even table?
- What will a 10x50 table reduce to?
- Did you notice that for our 3x5 table the ball passed through every cell in the table? Is that always true? Can you find a rule that governs this?Since ball travels integral table lengths, the number of cells traversed must be multiple of m. Similarly multiple of n. Hence multiple of nm if n and m do not have common factors. But N can anyway not be larger than nm. Hence, if n and m are coprime, then the ball must travel every square.If n and m have a common factor (like in even by even tables), then the table is reducible to a smaller table, and hence the ball MUST skip certain cells. Specifically, if d is the GCD of n and m, such that n=ad, and m=bd, then the ball must travel abd cells.
- What happens if the ball doesn't start at a corner but at another point?What color grid points does the ball traverse?If a ball starts at a corner, where will it end up?If n and m are even, and the ball starts on a white cell, what will happen? Think about it in terms of 2x2 cells to reduce the table.
.png)
Jokes
- What is the area of a circlepi.r^2 - No, "Pie are round, Crackers are square"
- What is the volume of a pizza with radius z and height a?pi.z.z.a
Homework
- Simpson Paradox: When one analyzes the voting records of democrats and republicans during the American Civil Rights Act, 1964, following facts emergeIn the northern states, 94% of Democrats voted for the act, compared with 85% of RepublicansIn the southern states, 7% of the Democrats voted for the act, compared to 0% of RepublicansWho showed more support for the act - Democrats or Republicans?Answer: Consider the following:
.png) What causes this non-intuitive answer? While there is abysmal voting by republicans in south, there are only 10 of them, so even if one vote had swung, it would look like 10%. On the other hand, there are lot of democrats in South, but very low support.
What causes this non-intuitive answer? While there is abysmal voting by republicans in south, there are only 10 of them, so even if one vote had swung, it would look like 10%. On the other hand, there are lot of democrats in South, but very low support.
References:
The Moscow Puzzles, by Boris A. Kordemsky
The Simpsons and their Mathematical Secrets, by Simon Singh